Branches and Bifurcations – Building a framework for modelling with isosurfaces in Generative Components

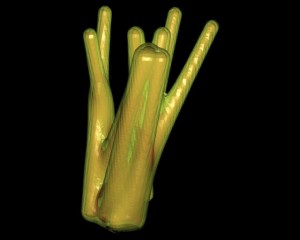
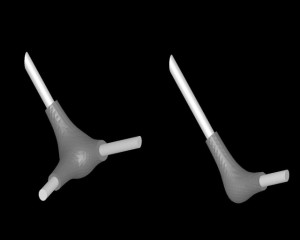
Abstract for eCAADe 2006 by Mirco Becker

Two nested isosurfaces – Copyright by Mirco Becker

An isosurface is a three-dimensional representation of a constant value of a field function within a given volume. They are normally used in computer graphics to visualize data in fluid dynamics, medical imaging, geophysics, and meteorology. The advantage of isosurfaces is that they can represent all sorts of topologies. That makes them a perfect tool for modeling, branching, forking, and bifurcating objects with smooth transitions. As they work of a field function, the surface is implicit, the polygonization an approximation. This is a good base for coupling performance with precision. The task was to define a set of handles to change and model an isosurface. It had to happen through the modeling of the field function in a way that is rather intuitive but without giving up the precision one is used to have from standard NURBS/BREP modeling.

Joint detail generated with isosurfaces based on linear field emitters. Copyright by Mirco Becker

The paper shows how a modeling framework for isosurfaces is implemented as a plug-in for Bentley Systems Generative Components allowing an intuitive way of exploring design variations. The implementation is illustrated with a proof of concept showing a sketch design

Journal Article: Communicating Space(s) [24th eCAADe Conference Proceedings / ISBN 0-9541183-5-9] Volos (Greece) 6-9 September 2006, pp. 868-873 DOI: 2006_868